
The dependent variable could be in seconds, in which case you would not say that the confidence interval is between 2.1 and 4.1 percent, you would say it is between 2.1 and 4.1 seconds. However, most studies do not have dependent variables in units of percentages. In the Strohmetz chocolate study, the dependent variable is in units of percentages because the researchers are studying tip percentages. These results support the researchers' hypothesis. The 95% confidence interval for the effect of chocolate on tip percentage is between 2.1 and 4.1 percent. On average, customers given chocolate tipped 17.7 percent, while customers not given chocolate tipped 14.6 percent. Tip percentages for the two groups differed significantly according to Welch's t-test, t(74.87) = 6.2, p <. Researchers hypothesized that giving customers chocolate with their bill would increase the tips that waiters received. To write up the results of this analysis, you could write: This means that it is highly unlikely that the two groups are equal. The p-value indicates that a t value more extreme than 6.2 occurs less than 1 out of a thousand times under the null distribution (assuming no difference between the two groups). The t statistic is 6.20, the df (degrees of freedom) is 74.87, and the p-value is less than. Serving customers chocolate with their check will increase your tip percentage somewhere between 2 and 4%. As before, the confidence interval allows you to know the precision of your estimate. You can be 95% confident that the difference between the population means for the Chocolate and No Chocolate conditions is somewhere between 2.11% and 4.12%. Welch's t-test output adds a calculation of the difference between the means of the two groups - 3.12% in tips - and also the confidence interval for that difference: 2.11 to 4.12. The standard deviations reported in the descriptive statistics confirm your earlier observation that the tip percentage is more spread out in the Chocolate condition (SD = 2.90) than in the No Chocolate condition (SD = 1.79). Here are the results for the t-test (in Element View): If you want less clutter on your screen, you can click the "Element View" tab in the output console to hide the red R command syntax. It is safer to make the assumption of unequal variances and use Welch's method, which reports a more unbiased estimate of p.Īfter you enter the appropriate variables into "Factor" (the independent variable in your study) and "Outcomes" (the dependent variable in your study) and click Run, you should get two pieces of output: the descriptive statistics for the two groups in your test and the results of the t-test. If the variance of the two groups is different, then the p-value reported by Student's t-test will be artificially high or low. The "Unequal Variance (Welch)" method will work whether your two groups have similar or dissimilar variance, whereas the other option (Student's t-test) is only valid when the two groups have approximately equal variance. Equal and unequal variance refer to the variances of the two groups you are comparing. Variance is a measure of dispersion, or how spread out the scores are. The default setting is "Unequal Variance (Welch) (Recommended)", and that is the one that I recommend as well. If you click on the icon of a gear that is to the right of the t-test checkbox, a dialog opens allowing you to choose between two different forms of the t-test.
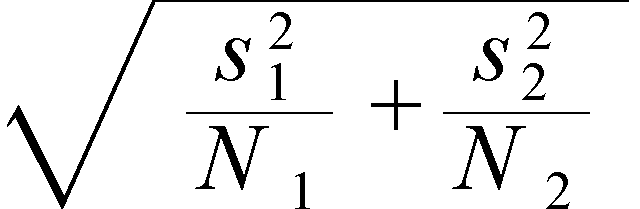
If your data includes outliers, you should consider using the Wilcoxon test (pictured on the right), which is not sensitive to outliers. For example, the icons below the t-test indicate that it assumes "Large Sample" (icon of a large letter "N") and "No Outliers" (icon of a red dot far from the rest of a scatterplot). Holding the mouse over the icon will cause text to appear showing you what assumption is indicated. These are a reminder of the assumptions of each test. You might notice the icons below each test: The default test statistic is the one we want: the t-test. To access these tests, select Analysis -> Two Sample Test. Plotting the data is a good way to get a feel for differences between groups, but statistics can provide us with two more pieces of information: a confidence interval for the difference between means and a measure of the probability that an effect is due to chance (statistical significance).


 0 kommentar(er)
0 kommentar(er)
